ESTADISTICA E INVESTIGACIÓN: 2010

jueves, 26 de agosto de 2010

DISTRIBUCIÓN T-STUDENT

/meta>

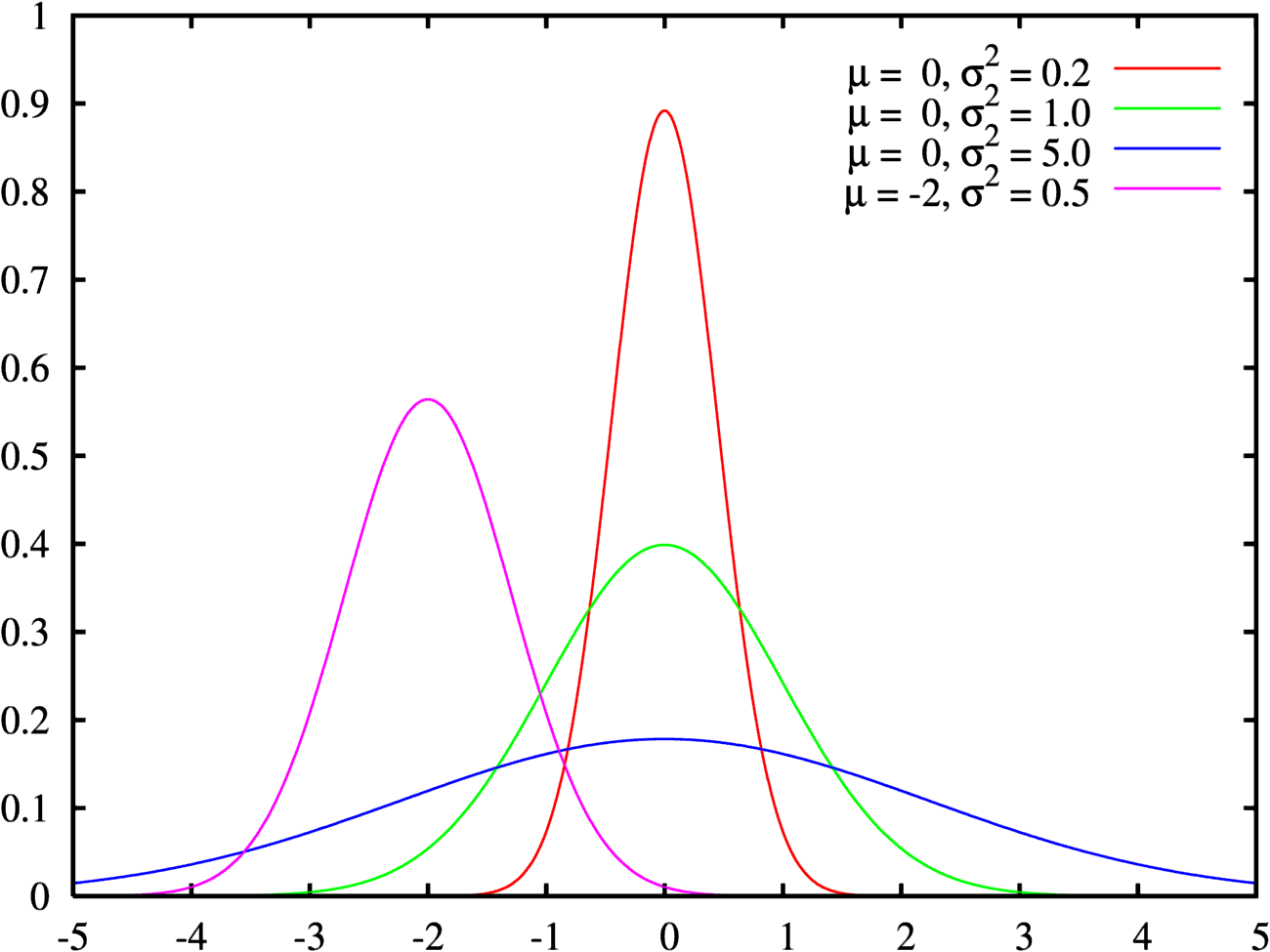
En probabilidad y estadística, la distribución t-Student es una distribución de probabilidad que surge del problema de estimar la media de una población normalmente distribuida cuando el tamaño de la muestra es pequeño. Se utiliza entonces para hacer inferencia con respecto a una o dos medias poblacionales.

La distribución t-Student se construye como un cociente entre una normal y la raíz de una $\chi ^2$ independientes. De modo preciso, llamamos distribución t-Student con n grados de libertad, ${ {{\bf t} } }_{n}$ a la de una v.a. T,
$\begin{displaymath}{ \mbox{\fbox{$\displaystyle T=\frac{Z}{\sqrt{ \frac{1}{n}\chi_n^2}} {\leadsto}{ {{\bf t} } }_n $ } } } \end{displaymath}$

donde $Z{\leadsto}{ {{\bf N} \left( 0,1 \right)} }$ , $\chi_n^2{\leadsto}{ \mbox{\boldmath$\chi$ } }_n^2$ . Este tipo de distribuciones aparece cuando tenemos n+1 v.a. independientes

$\begin{displaymath}X{\leadsto}{ {{\bf N} \left( \mu,\sigma^2 \right)} } \end{displaymath}$

$\begin{displaymath}X_i{\leadsto}{ {{\bf N} \left( \mu_i,\sigma_i^2 \right)} }\qquad i=1,\dots,n \end{displaymath}$

y nos interesa la distribución de

$\begin{displaymath}T=\frac{ \displaystyle \frac{X-\mu}{\sigma}}{ \sqrt{\displays... ...c{X_i-\mu_i}{\sigma_i} \right)^2 }} {\leadsto}{ {{\bf t} } }_n \end{displaymath}$

Una variable aleatoria se distribuye según el modelo de t-Student con n grados de libertad, donde n es un entero positivo, si su función de densidad es la siguiente: $t_n{\leadsto}{ {{\bf t} } }_n$ es

$\begin{displaymath}f_T(x)=\frac{\Gamma\left(\frac{n+1}{2}\right)}{\Gamma\left( \... ...ac{x^2}{n}\right)^{-\frac{n+1}{2}} \qquad \forall\,t\in I\!\!R \end{displaymath}$

**Figura:** Función de densidad de una t de Student
$\includegraphics[angle=-90, width=0.8\textwidth]{fig06-16.epsi}$

La distribución ${ {{\bf t} } }$ de Student tiene propiedades parecidas a ${ {{\bf N} \left ( 0,1 \right )} }$ :

Es de media cero, y simétrica con respecto a la misma;
Es algo más dispersa que la normal, pero la varianza decrece hasta 1 cuando el número de grados de libertad aumenta;

Figura: Comparación entre las funciones de densidad de ${ {{\bf t} } }_1$ y ${ {{\bf N} \left ( 0,1 \right )} }$ .

$\includegraphics[angle=-90, width=0.8\textwidth]{fig06-17.epsi}$
Para un número alto de grados de libertad se puede aproximar la distribución de Student por la normal, es decir,

$\begin{displaymath}{ {{\bf t} } }_n \stackrel{n\rightarrow \infty}{\longrightarrow} { {{\bf N} \left( 0,1 \right)} } \end{displaymath}$

Figura: Cuando aumentan los grados de libertad, la distribución de Student se aproxima a la distribución normal tipificada.

$\includegraphics[angle=-90, width=0.8\textwidth]{fig06-18.epsi}$
Para calcular

$\begin{displaymath}{{\cal P}}[T\leq t] = F_T(t) = \int_{-\infty}^t f_T(x)\,dx = ... ...qrt{n\pi}} \left(1+\frac{x^2}{n}\right)^{-\frac{n+1}{2}}\, dx} \end{displaymath}$

en lugar de considerar una primitiva de esa función y determinar la integral definida, buscaremos el resultado aproximado en una tabla de la distribución ${ {{\bf t} } }_{n}$ . Véase la tabla 4, al final del libro.

**Figura:** Comparación entre las funciones de densidad de ${ {{\bf t} } }_1$ y ${ {{\bf N} \left ( 0,1 \right )} }$ .
$\includegraphics[angle=-90, width=0.8\textwidth]{fig06-17.epsi}$

**Figura:** Cuando aumentan los grados de libertad, la distribución de Student se aproxima a la distribución normal tipificada.
$\includegraphics[angle=-90, width=0.8\textwidth]{fig06-18.epsi}$

Referencia: www.bioestadistica.uma.es/libro/node81.htm

MODELOS DE PROBABILIDAD CONTINUOS: NORMAL Y T-STUDENT

En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece en fenómenos reales.
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro. Esta curva se conoce como campana de Gauss.
La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos.
La distribución normal también es importante por su relación con la estimación por mínimos cuadrados, uno de los métodos de estimación más simples y antiguos.
Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:

caracteres morfológicos de individuos como la estatura;
caracteres fisiológicos como el efecto de un fármaco;
caracteres sociológicos como el consumo de cierto producto por un mismo grupo de individuos;
caracteres psicológicos como el cociente intelectual;
nivel de ruido en telecomunicaciones;
errores cometidos al medir ciertas magnitudes;
etc.

La distribución normal también aparece en muchas áreas de la propia estadística. Por ejemplo, la distribución muestral de las medias muestrales es aproximadamente normal, incluso si la distribución de la población de la cual se extrae la muestra no es normal.^[1] Además, la distribución normal maximiza la entropía entre todas las distribuciones con media y varianza conocidas, lo cual la convierte en la elección natural de la distribución subyacente a una lista de datos resumidos en términos de media muestral y varianza. La distribución normal es la más extendida en estadística y muchos tests estadísticos están basados en una supuesta "normalidad".
En probabilidad, la distribución normal aparece como el límite de varias distribuciones de probabilidad continuas y discretas.
Las características que descacan a este distribución son: que el dominio de la variable va desde -oo hasta +oo; su curva es simétrica respecto de la media; la distribución es Unimodal por lo que la media, mediana y moda son iguales; por cada cambio en la media la curva se desplaza hacia la derecha o izquierda; y por cambios en la varianza y/o desviación estándar la curva cambia de forma, es decir se puede achatar si la varianza es grande y ser mas puntiaguda si la varianza es pequeña (ver gráfico siguiente).
REFERENCIA: http://es.wikipedia.org/wiki/Distribuci%C3%B3n_normal.

MODELOS DE PROBABILIDAD NORMAL

http://upload.wikimedia.org/wikipedia/commons/1/1b/Normal_distribution_pdf.png

MODELOS DE PROBABILIDAD DISCRETOS

Los modelos o distribuciones de probabilidad más usados o más conocidos son:
- Uniforme
- Binomial
- Hipergeométrico
- Poisson
El modelo Binomial: se utiliza en experimentos aleatoros donde la variable en estudio es discreta, existen sólo dos posibles resultados: Éxito y Fracaso. La probabilidad de éxito se conoce como p y la probabilidad de fracaso como (1-p). Cuando se realiza el experimento y el muestreo es Con Reposición se puede aplicar este modelo binomial por lo que los eventos que se generan son independientes. La calificación de éxito o frecaso a un determinado hecho depende del interés del investigador. La curva de la distribución es Asimétrica positiva. Ejemplos de experimentos binomiales:
* Presentar un examen (éxito=aprobar, fracaso =reprobar)
* Conseguir empleo
* Viajar al exterior
* Conseguir la información que se busca

El modelo Hipergeométrico: cuando el muestreo se realiza Sin Reposición se puede aplicar este modelo por lo que los puntos muestrales que se originan y que forman los eventos son dependientes, la variable en estudio es discreta, se caracteriza principalmente porque existen un número determinado de elementos que presentan cierta característica.

El modelo de Poisson: se usa para análisis de variables aleatorias discretas medidas en el tiempo o en el espacio (tiempo: días, horas, minutos, segunddos, semanas, meses; espacio: km. cm. cc. mts..); los puntos muestrales o eventos que se generan en una unidad de tiempo o espacio son independientes de los que ocurren en otra unidad de tiempo o espacio; el promedio o tasa de eventos que ocurren en una unidad de tiempo o espacio es proporcional al cambio de la unidad de tiempo o espacio. cuando el tamaño de la muestra es grande (n>30) y la probabilidad de éxito es muy pequeña, se puede usar el modelo de Piosson en lugar del Modelo Binomial usando el promedio del modelo binomila como parámetro de Poisson. para mayor información visitar: http://es.wikipedia.org/wiki/Distribuci%C3%B3n_de_Poisson

miércoles, 26 de mayo de 2010

PARÁMETROS

Los parámetros son los valores que caracterizan a una población de individuos entes o cosas. Por ejemplo el promedio, la mediana, la moda, la desviación estándar, la proporción, entre otros. Por lo general los parámetros se desconocen y se estiman a través de los estadígrafos. El desconocimiento de un parámetro tiene que ver con las variables que se este interesado en analizar en una investigación y además del tamaño de dicha población. casi siempre sucede que las pobalciones bajo estudio son grandes y se requiere de recursos económicos, humanos y tecnológicos para recaudarla, es recomendable tomar muestras; en consecuencia los parámetros son desconocidos y por ende son estimados.

ESTADÍGRAFO

Un estadígrafo o Estadístico es una función matemática que utiliza datos de muestra para llegar a un resultado que debe ser un número real. Los Estadígrafos son utilizados para estimar parámetros o como valores de distribuciones de probabilidad que permiten hacer inferencia estadística (la inferencia estadística son los contrastes de hipótesisi y los intervalos de confianza de uno o varios paámetros)

viernes, 30 de abril de 2010

VARIABLE ALEATORIA

Una variable aleatoría es una función que a cada evento del espacio muestral, le asigna un número real, entonces se dice que va del espacio muestral al conjunto R. Las variables aleatorias se originan de un experimento aleatorio y pueden ser discretas o continuas. Sea cual sea el tipo de v.a. tiene una función de probabiliad, un valor esperado o promedio y la variabilidad con que ocurre los valores asignados.
Por tanto se tiene que:
La función de probabilidad contiene cada una de la probabilidades de cada valor distinto que la función asigna a los eventos del espacio muestra, se denota para el caso discreto como P(X=xi), y se puede colocar en un arreglo de filas y columnas a saber:

Valor que la función X le asigna a cada evento	X=xi	x1	x2	x3……..	xn	Total
Función de Probabilidad	P(X=xi)	P1	P2	P3……..	Pn	1
Función de Distribución	F(X)	P(X≤x1)	P(X≤x2)	P(X≤x3)…..	1

Valor esperado o esperanza matemática:

μ=E(X)=∑[xi*P(X=xi)]
varianza:

varianza =E(x^2 )-E(x)=∑[〖xi〗^2*P(X=xi) ] -∑[xi*P(X=xi)]

jueves, 15 de abril de 2010

Estadística Inferencial o Inductiva

La estadistica inferencial utiliza datos provenientes de una muestra para obtener resultados que se infieren a toda la población; por ejemplo si dada una muestra de 20 de una población de 450 individuos y se obtiene que el ingreso promedio muestral es de 2.500,oo Bs.F., entonces se dice que la población de 450 individuos gana en promedio 2.500,oo Bs. F.

domingo, 11 de abril de 2010

Teoremas Básicos de Probabilidad

1.- P(Ω)=1
2.- P(ø) =0

3.- Si AЄΩ y Ac es el complemento de A:
              P(A) +P(Ac) = P(Ω) =1. Por tanto:
      3.1.- P(Ac)= 1-P(A)

4.- Si A, B Є Ω puede suceder que:
      4.1.- A y B sean excluyentes; en este caso:
               P(AóB)=P(AUB)=P(A)+P(B)
      4.2.- A y B Є Ω y NO sean excluyentes:
              P(A ó B)=P(A∪B)=P(A)+P(B)-P(A∩B)

Si A, B y C Є Ω y no son excluyentes:
         P(A∪B∪C)=P(A)+P(B)+P(C)-P(A∩B)-P(A∩C)-P(B∩C)+P(A∩B∩C)

5.- Si A, B y C Є Ω y además son independientes:
      P(A∩B∩C)=P(A)*P(B)*P(C)
(OJO: dos o más eventos pueden ser independientes y estar o no interceptados)

6.- Si A, B y C Є Ω y son eventos dependientes:
                          P(A∩B∩C)=P(A)*P(B⁄A)*P(C⁄(A∩B))

7.- Si A, B Є Ω y son eventos condicionados:
      La probabilidad de A dado que B ocurrió es:
      P(A⁄B)=(P(A∩B))/(P(B)) ; esto es si B ocurrió primero que A.
      La probabilidad de B dado que A ocurrió es:
      P(B⁄A)=(P(A∩B))/(P(A)); esto es si A ocurrió primero que B.

viernes, 9 de abril de 2010

Conceptos Básicos de Probabilidad

Probabilidad: un número que refleja que tan posible un hecho puede ocurrir.

Experimento Aleatorio: utilizado en situaciones bajo incertidumbre, se puede aplicar a situaciones de la vida en cualquier áre; y debe satisfacer las siguientes condiciones: a) el experimiento se puede realizar 1 o más veces; b) se pueden conocer por adelantado sus resultados; c)no se puede asegurar antes de la realización del experimento cual será el resultado particular a obtener. Los ejemplos más sencillos utilizados para reflejar esta situación son: los juegos de azar (lanzamientos de monedas, dados, etc.).

Espacio muestral: es el conjunto de todos los posibles resultados que origina un experimento aleatorio. Evento: es un hecho o suceso que podría ocurrir y que está asociado a un experimento aleatorio.

Clasificación de Eventos: i) Simples si contiene un solo punto muestral o n solo evento; ii) Compuesto si contiene más de un punto muestral o eventos.
Tipos de Eventos:
Vacio: no contiene puntos muestrales. Posible: cualquier evento contenido en el espacio muestral.
Imposible: No puede ocurrir o está fuera del espacio muestral.
Favorable: esta definido bajo una condición o premisa.
Unión: si dos eventos A y B pertenecen al espacio muestral, la unión de ellos es el resultado de unir los puntos muestrales o eventos que estan en el conjunto A o en el B o en ambos.
Intercepción: si dos eventos A y B pertenecen al espacio muestral, la intercepción de ellos son los puntos muestrales que están tanto en A como en B.
Excluyentes: dos o más eventos son excluyentes si no tienen nada en común (no están interceptados) o no ocurren simultaneamente.
Exahustivos: dos o mas eventos son exahustivos si al unirlos su resultado es el espacio muestral. Independiantes: dos o más eventos son independientes si la ocurrencia de uno no afecta la ocurrencia de otro(s).
Dependientes: dos o más eventos son dependientes si la ocurrencia de uno afecta la ocurrencia de otro(s). Condicionados: dos o más eventos están condicionados si primero debe ocurrir uno de ellos para que puedan ocurrir los demás.

lunes, 29 de marzo de 2010

Muestreo

El muestreo es el procedimiento que permite calcular el valor de una muestra.
Si el muestreo es probabilista, el procedimiento es estadístico basado en la teoría de las probabilidades.
si el muestreo no es probabilista, el procedimiento no involucra las probabilidades
los muestreos probabilistas pueden ser:
a) Aleatorio Simple
b) Sistemático
C) Estratificado
d) por conglomerados
Los muestreos no probabilistas pueden identificarse como:
a) Intencional
B) Opinático
c) Bola de nieve
d) Cuotas, entre otros

sábado, 20 de febrero de 2010

Probabilidad

La teoría de las probabilidades son un conjunto de métodos y procedimientos que permiten visualizar el futuro incierto, para hacer uso de ella es necesario establecerse un experimento de la vida real y proceder a identificar que es lo que nos interesa analizar. a partir de allí se puede establecer con que modelo de probabilidad se puede analizar nuestro experimento, que por supuesto tiene que ser aleatorio. Es decir, se puede realizar 1 o más veces, se conocen los posibles resutlados; pero no se puede asegurar cual se obtendra en una realización particular del experimento... la utilidad de las probabilidades le permite a las personas calcular la posibilidad de que un hecho ocurra en un futuro...

ESTADISTICA E INVESTIGACIÓN